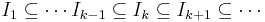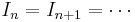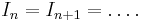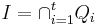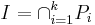Noetherian ring

In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element. Equivalently, a ring is Noetherian if it satisfies the ascending chain condition on ideals; that is, given any chain:

$I_1\subseteq\cdots I_{k-1}\subseteq I_{k}\subseteq I_{k%2B1}\subseteq\cdots$

there exists a positive integer n such that:

$I_{n}=I_{n%2B1}=\cdots$

There are other equivalent formulations of the definition of a Noetherian ring and these are outlined later in the article.

The notion of a Noetherian ring is of fundamental importance in both commutative and noncommutative ring theory, due to the role it plays in simplifying the ideal structure of a ring. For instance, the ring of integers and the polynomial ring over a field are both Noetherian rings, and consequently, such theorems as the Lasker–Noether theorem, the Krull intersection theorem, and the Hilbert's basis theorem hold for them. Furthermore, if a ring is Noetherian, then it satisfies the descending chain condition on prime ideals. This property suggests a deep theory of dimension for Noetherian rings beginning with the notion of the Krull dimension.

1 Introduction
2 Characterizations
3 Hilbert's basis theorem
4 Primary decomposition
5 Uses
6 Examples
7 Properties
8 References

Introduction

Let $\mathbb{Z}$ denote the ring of integers; that is, let $\mathbb{Z}$ be the set of integers equipped with its natural operations of addition and multiplication. An ideal in $\mathbb{Z}$ is a subset, I, of $\mathbb{Z}$ that is closed under subtraction (i.e., if 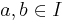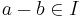$a,b\in I$ , $a-b\in I$ ), and closed under "inside-outside multiplication" (i.e., if r is any integer, not necessarily in I, and i is any element of I, 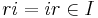$ri=ir\in I$ ). In fact, in the general case of a ring, these two requirements define the notion of an ideal in a ring. It is a fact that the ring $\mathbb{Z}$ is a principal ideal ring; that is, for any ideal I in $\mathbb{Z}$ , there exists an integer n in I such that every element of I is a multiple of n. Conversely, the set of all multiples of an arbitrary integer n is necessarily an ideal, and is usually denoted by (n).

Although there are many (equivalent) formulations of what it means for a ring, R, to be Noetherian, one formulation dictates that any ascending chain of ideals in R terminates. That is, if:

$I_1\subseteq\cdots I_{k-1}\subseteq I_{k}\subseteq I_{k%2B1}\subseteq\cdots$

is an ascending chain of ideals, then there exists a positive integer n such that

$I_{n}=I_{n%2B1}=\ldots.\$

For instance, if I and J are ideals in $\mathbb{Z}$ , there exists integers n and m such that I=(n) and J=(m) (i.e., every integer in I is a multiple of n and every integer in J is a multiple of m). In this case, 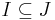$I\subseteq J$ if and only if every element of I is an element of J, or equivalently, if every multiple of the integer n is a multiple of m. In other words, 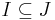$I\subseteq J$ if and only if m divides n (or m is a factor of n). Furthermore, the inclusion 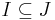$I\subseteq J$ is proper if and only if m is a proper divisor of n (i.e., 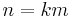$n=km$ with k not equal to either 1 or −1).

Thus, if:

$I_1\subseteq\cdots I_{k-1}\subseteq I_{k}\subseteq I_{k%2B1}\subseteq\cdots$

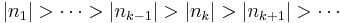is an ascending chain of ideals in $\mathbb{Z}$ and I_j=(n_j) for all j and integers n_j, n_j+1 divides n_j for all j. If each inclusion is proper (that is, if the chain does not terminate), n₂ would be a proper divisor of n₁, n₃ would be a proper divisor of n₂ etc. In particular, $|n_1|>\cdots>|n_{k-1}|>|n_k|>|n_{k%2B1}|>\cdots$ which is impossible since there can only be finitely many positive integers strictly less than n₁. Consequently, $\mathbb{Z}$ is a Noetherian ring.

For this reason, the notion of a Noetherian ring generalizes such rings as $\mathbb{Z}$ . The fundamental property of $\mathbb{Z}$ used in the proof above is that there cannot be a chain of positive integers where each integer in the chain is strictly less than its predecessor; in other words, the ring of integers is not "too large" since it cannot sustain such a "large chain". This is typical in the theory of Noetherian rings; often, to prove a result about Noetherian rings, one appeals to the fact that the rings in question are not "too large". More formally, one assumes that the conclusion of the result is false and exhibits an ascending chain that does not terminate thus contradicting the fact that the ring is "not too large", and establishing that the conclusion must, in fact, be true.

While the proof that $\mathbb{Z}$ is a Noetherian ring uses the order structure of $\mathbb{Z}$ , typical proofs in ring theory in general do not assume such additional structure on the ring. In fact, it is possible to give a proof that $\mathbb{Z}$ is a Noetherian ring without appealing to its order structure and this proof applies more generally to principal ideal rings (i.e., rings in which every ideal is generated by a single element).

Although the ring $\mathbb{Z}$ is a Noetherian ring, the theory of Noetherian rings extends far beyond just this ring. For example, let $\mathbb{Z}[X]$ denote the polynomial ring in one indeterminant over $\mathbb{Z}$ . More specifically, let $\mathbb{Z}[X]$ be the set of all polynomials with integer coefficients (such a polynomial is also referred to as a polynomial over $\mathbb{Z}$ ), with addition and multiplication defined to be natural polynomial addition and multiplication. Under these operations $\mathbb{Z}[X]$ becomes a ring. More generally, if R is any ring, the set of all polynomials with coefficients in R can be equipped with the structure of a ring and is denoted by R[X].

Although every ideal in $\mathbb{Z}$ is simply the set of multiples of a certain integer n, the ideal structure of $\mathbb{Z}[X]$ is slightly more complicated; there are ideals that may not be expressed as the set of multiples of a given polynomial. Put differently, $\mathbb{Z}[X]$ is not a principal ideal ring. However, it is a Noetherian ring. This fact follows from the famous Hilbert's basis theorem named after mathematician David Hilbert; the theorem asserts that if R is any Noetherian ring (such as, for instance, $\mathbb{Z}$ ), R[X] is also a Noetherian ring. In fact, by the principle of mathematical induction, Hilbert's basis theorem establishes that $\mathbb{Z}[X_1,\cdots,X_n]$ , the ring of all polynomials in n variables with coefficients in $\mathbb{Z}$ , is a Noetherian ring.

Thus, in a sense, the notion of a Noetherian ring unifies the ideal structure of various "natural rings". While the ideal structure of $\mathbb{Z}[X_1,\cdots,X_n]$ becomes considerably more complex as n increases, the rings in question still remain Noetherian, and any theorem about $\mathbb{Z}$ that can be proven using only the fact that $\mathbb{Z}$ is Noetherian, can be proven for $\mathbb{Z}[X_1,\cdots,X_n]$ .

Characterizations

For noncommutative rings, it is necessary to distinguish between three very similar concepts:

A ring is left-Noetherian if it satisfies the ascending chain condition on left ideals.
A ring is right-Noetherian if it satisfies the ascending chain condition on right ideals.
A ring is Noetherian if it is both left- and right-Noetherian.

For commutative rings, all three concepts coincide, but in general they are different. There are rings that are left-Noetherian and not right-Noetherian, and vice versa.

There are other, equivalent, definitions for a ring R to be left-Noetherian:

Every left ideal I in R is finitely generated, i.e. there exist elements a₁, ..., a_n in I such that I = Ra₁ + ... + Ra_n.
Every non-empty set of left ideals of R, partially ordered by inclusion, has a maximal element with respect to set inclusion.

Similar results hold for right-Noetherian rings.

It is also known that for a commutative ring to be Noetherian it suffices that every prime ideal of the ring is finitely generated. (The result is due to I. S. Cohen.)

Hilbert's basis theorem

Main article: Hilbert's basis theorem

If R is a ring, let R[X] denote the ring of polynomials in the indeterminant X over R. Hilbert proved that if R is "not too large", in the sense that if R is Noetherian, the same must be true for R[X]. Formally,

Theorem

If R is a Noetherian ring, then R[X] is a Noetherian ring.

Corollary

If R is a Noetherian ring, then $R[X_1,\cdots,X_n]$ is a Noetherian ring.

For a proof of this result, see the corresponding section on the Hilbert's basis theorem page. Geometrically, the result asserts that any infinite set of polynomial equations may be associated to a finite set of polynomial equations with precisely the same solution set (the solution set of a collection of polynomials in n variables is generally a geometric object (such as a curve or a surface) in n-space).

Primary decomposition

Main article: Lasker–Noether theorem

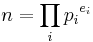In the ring $\mathbb{Z}$ of integers, an arbitrary ideal is of the form (n) for some integer n (where (n) denotes the set of all integer multiples of n). If n is non-zero, and is neither 1 nor −1, by the fundamental theorem of arithmetic, there exist primes p_i, and positive integers e_i, with $n=\prod_{i} {p_i}^{e_i}$ . In this case, the ideal (n) may be written as the intersection of the ideals (p_i^e_i); that is, 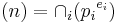$(n)=\cap_{i} ({p_i}^{e_i})$ . This is referred to as a primary decomposition of the ideal (n).

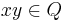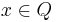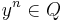In general, an ideal Q of a ring is said to be primary if Q is proper and whenever $xy\in Q$ , either $x\in Q$ or $y^n\in Q$ for some positive integer n. In $\mathbb{Z}$ , the primary ideals are precisely the ideals of the form (p^e) where p is prime and e is a positive integer. Thus, a primary decomposition of (n) corresponds to representing (n) as the intersection of finitely many primary ideals.

Since the fundamental theorem of arithmetic applied to a non-zero integer n that is neither 1 nor −1 also asserts uniqueness of the representation 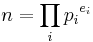$n=\prod_{i} {p_i}^{e_i}$ for p_i prime and e_i positive, a primary decomposition of (n) is essentially unique.

For all of the above reasons, the following theorem, referred to as the Lasker–Noether theorem, may be seen as a certain generalization of the fundamental theorem of arithmetic:

Theorem

Let R be a Noetherian ring and let I be an ideal of R. Then I may be written as the intersection of finitely many primary ideals with distinct radicals; that is:

$I=\cap_{i=1}^t Q_i$

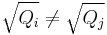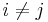with Q_i primary for all i and $\sqrt{Q_i}\neq\sqrt{Q_j}$ for $i\neq j$ . Furthermore, if:

$I=\cap_{i=1}^k P_i$

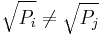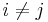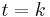is decomposition of I with $\sqrt{P_i}\neq\sqrt{P_j}$ for $i\neq j$ , and both decompositions of I are irredundant (meaning that no proper subset of either $\{Q_1,\dots,Q_t\}$ or $\{P_1,\dots,P_k\}$ yields an intersection equal to I), $t=k$ and (after possibly renumbering the Q_i's) 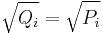$\sqrt{Q_i}=\sqrt{P_i}$ for all i.

For any primary decomposition of I, the set of all radicals, that is, the set 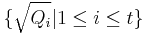$\{\sqrt{Q_i}|1\leq i\leq t\}$ remains the same by the Lasker–Noether theorem. In fact, it turns out that (for a Noetherian ring) the set is precisely the assassinator of the module R/I; that is, the set of all annihilators of R/I (viewed as a module over R) that are prime.

Uses

The Noetherian property is central in ring theory and in areas that make heavy use of rings, such as algebraic geometry. The reason behind this is that the Noetherian property is in some sense the ring-theoretic analogue of finiteness. For example, the fact that polynomial rings over a field are Noetherian allows one to prove that any infinite set of polynomial equations can be replaced with a finite set with the same solutions.

Krull's principal ideal theorem is an important property of Noetherian rings. It states that every principal ideal in a commutative Noetherian ring has height one; that is, every principal ideal is contained in a prime ideal minimal amongst nonzero prime ideals. This early result was the first to suggest that Noetherian rings possessed a deep theory of dimension.

Examples

Any field, including fields of rational numbers, real numbers, and complex numbers. (A field only has two ideals — itself and (0).)
Any principal ideal domain, such as the integers.
The ring of polynomials in finitely-many variables over the integers or a field.

Rings that are not Noetherian tend to be (in some sense) very large. Here are two examples of non-Noetherian rings:

The ring of polynomials in infinitely-many variables, X₁, X₂, X₃, etc. The sequence of ideals (X₁), (X₁, X₂), (X₁, X₂, X₃), etc. is ascending, and does not terminate.
The ring of continuous functions from the real numbers to the real numbers is not Noetherian: Let I_n be the ideal of all continuous functions f such that f(x) = 0 for all x ≥ n. The sequence of ideals I₀, I₁, I₂, etc., is an ascending chain that does not terminate.

However, a non-Noetherian ring can be a subring of a Noetherian ring:

The ring of rational functions generated by x and y/xⁿ over a field k is a subring of the field k(x,y) in only two variables.

Indeed, there are rings that are left Noetherian, but not right Noetherian, so that one must be careful in measuring the "size" of a ring this way.

Properties

If R is a Noetherian ring, then R[X] is Noetherian by the Hilbert basis theorem. Also, R[[X]], the power series ring is a Noetherian ring.
If R is a Noetherian ring and I is a two-sided ideal, then the factor ring R/I is also Noetherian.
Every finitely-generated commutative algebra over a commutative Noetherian ring is Noetherian. (This follows from the two previous properties.)
Every localization of a commutative Noetherian ring is Noetherian.
A consequence of the Akizuki-Hopkins-Levitzki Theorem is that every left Artinian ring is left Noetherian. Another consequence is that a left Artinian ring is right Noetherian if and only if right Artinian. The analogous statements with "right" and "left" interchanged are also true.
A ring R is left-Noetherian if and only if every finitely generated left R-module is a Noetherian module.
A left Noetherian ring is left coherent and a left Noetherian domain is a left Ore domain.
A ring is (left/right) Noetherian if and only if every direct sum of injective (left/right) modules is injective. Every injective module can be decomposed as direct sum of indecomposable injective modules.

References

Chapter X of Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0

Noetherian ring

Contents

Introduction

Characterizations

Hilbert's basis theorem

Primary decomposition

Uses

Examples

Properties

References